简介
这篇论文主要提出一个新颖的非极大值抑制(Non-Maximum Suppression, NMS)算法更好地改善检测器给出的检测框。本文主要贡献:
- 提出adaptive-NMS,该算法根据目标的密度使用一个动态抑制阈值。
- 设计一个高效网络学习密度得分,这个得分可以方便地嵌入到single-stage和two-stage检测器中。
- 实现了CityPersons和CrowdHuman数据集上的 state of the art 结果。
Motivation

图1展示了不同阈值下的greedy-NMS的结果。蓝色的框表示丢失的目标,红色的框表示假正例(false positives)。(b)中的检测框是Faster R-CNN在NMS之前的检测结果。如图c,一个低的NMS阈值可能会移除正例(true positives)。如同d,一个高的NMS阈值可能会增加假正例(false positives)。
在本文中,作者提出了一种新的NMS算法,名为adaptive-NMS,它可以作为人群中行人检测的更有效的替代方案。直观地,高NMS阈值保持更多拥挤的实例,而低NMS阈值消除更多误报。因此,自适应NMS应用动态抑制策略,其中阈值随着实例聚集和相互遮挡而上升,并且当实例单独出现时衰减。为此,我们设计了一个辅助且可学习的子网络来预测每个实例的自适应NMS阈值。
Adaptive-NMS
当物体处于拥挤区域时,增加NMS的阈值可以保留高覆盖率。同样,在稀疏场景下,应该去掉重复度高的候选框,因为它们很可能是假正例。
\[ d_i:= \max_{b_j \in \mathcal{G}, i \neq j} \mathrm{iou}(b_i, b_j) \]
目标\(i\)的密度被定义和在ground truth集合\(\mathcal{G}\)中的其他目标的最大紧致框的IoU的值。目标的密度表示拥挤遮挡的程度。
使用这个定义,我们提出更新下面策略中的移除步骤,
\[ N_\mathcal{M} := \max(N_t, d_\mathcal{M}) \]
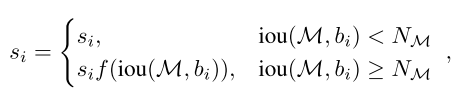
\(N_t\)表示对于\(\mathcal{M}\)的adaptive NMS的阈值,\(d_{\mathcal{M}}\)表示目标\(\mathcal{M}\)覆盖的密度。
这个抑制策略有三个性质: 1. 当相邻的框远离\(\mathcal{M}\)时,即\(\mathrm{iou}(\mathcal{M}, b_i) < N_t\),它们与原始NMS保持一致。 2. 如果\(\mathcal{M}\)定位到拥挤的区域,即\(d_{\mathcal{M}} > N_t\),\(\mathcal{M}\)的密度被使用作为adaptive NMS的阈值。 3. 对与稀疏区域的目标,即\(d_{\mathcal{M}} \leq N_t\),NMS阈值\(N_\mathcal{M}\)和原始NMS阈值相等,非常接近的框被作为假正例所抑制。
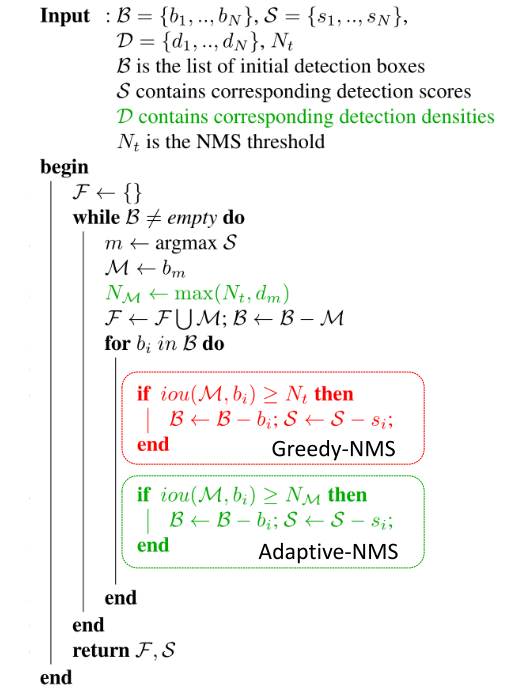
这个算法具体步骤如图2所示。
Density Prediction
作者把密度估计作为一个回归问题,目标密度值的计算根据它的定义,使用Smooth-L1损失函数作为训练损失。
一个天然的方式就是为这个回归在网络顶部添加一个并行的层,像分类和定位一样。然而,用于检测的特征仅仅包含目标自己的信息,比如外表、语义特征和位置。对于密度估计,使用独立目标的信息很难估计其密度,密度估计需要使用其周围目标的更多的线索。
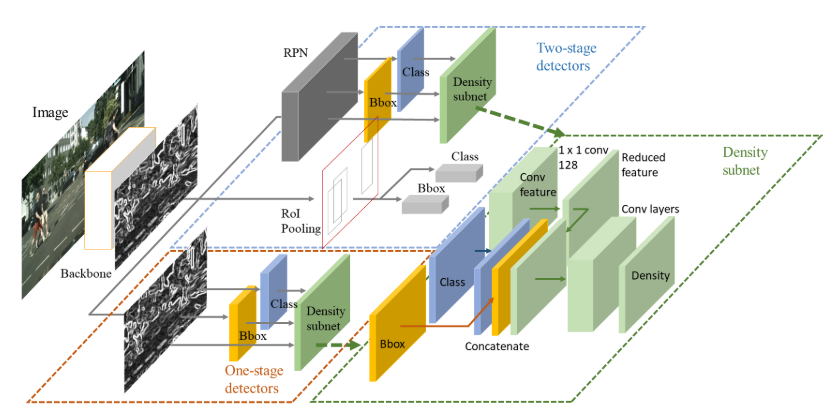
为了解决这个,作者设计了一个额外的网络,它由三层卷积层构成,如图3所示。首选使用一个1x1的卷积层做特征维度降维,然后级联降维后的特征、用于RPN分类的特征和用于RPN回归的特征。最后使用一个大尺度的卷积核5x5作为最后的卷积层,为了把周围的信息送入网络。具体如图中Density subnet绿色框区域结构。
Experiments