[MLIA] Logistic Regression

Posted on Edited on In Views:
Logistic Regression And Code

Logistic Regression

本代码来自Machine Learning in Action。

想要了解更多的朋友可以参考此书。

Sigmoid函数

\[\sigma(z) = \frac{1}{(1+e^{-z})}\]

1
2
3
4
5
6
7
8
9
10
import numpy as np
import matplotlib.pyplot as plt

def sigmoid(inX):
    return 1.0/(1+np.exp(-inX))

z = np.linspace(-5, 5, 100)
y = sigmoid(z)
plt.plot(z, y)
plt.show()
png 
1
2
3
4
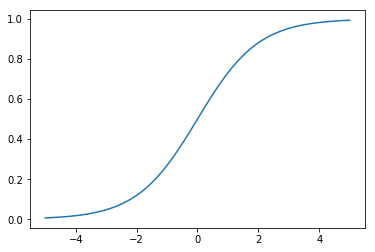
z = np.linspace(-60, 60, 100)
y = sigmoid(z)
plt.plot(z, y)
plt.show()
png

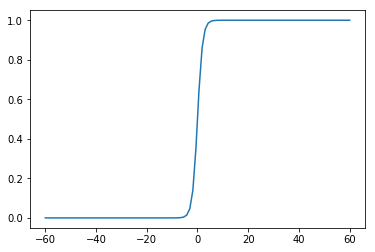
Sigmoid函数类似一个单位阶跃函数。当x＝0时，Sigmoid函数值为0.5；随着x增大，Sigmoid函数值将逼近于1；随着x减小，Sigmoid函数将逼近于0。利用这个性质可以对它的输入做一个二分类。

为了实现Logistic回归分类器，我们可以在每个特征上都乘以一个回归系数，然后把它的所有的结果值相加，将这个总和带入Sigmoid函数中，进而得到一个范围在0~1之间是数值。当大于0.5的时候，将数据分类为1；当小于0.5的时候，将数据分类为0。

Sigmoid函数的输入记为z:

\[z=w_0x_0 + w_1x_1 + w_2x_2 + \cdot \cdot \cdot + w_n x_n\]

Sigmoid函数的导数

Sigmoid导数具体推导过程如下：

\[ \begin{align} f^{\prime}(z) &= (\frac{1}{1+e^{-z}})^{\prime}\\\ &=\frac{e^{-z}}{(1+e^{-z})^2}\\\ &=\frac{1+e^{-z}-1}{(1+e^{-z})^2}\\\ &=\frac{1}{(1+e^{-z})}(1-\frac{1}{(1+e^{-z})})\\\ &=f(z)(1-f(z)) \end{align} \]

梯度上升法

梯度上升法：顾名思义就是利用梯度方向，寻找到某函数的最大值。

梯度上升算法迭代公式： \[w:=w+\alpha \nabla_w f(w)\]

梯度下降法：和梯度上升想法，利用梯度方法，寻找某个函数的最小值。 梯度下降算法迭代公式： \[w:=w-\alpha \nabla_w f(w)\]

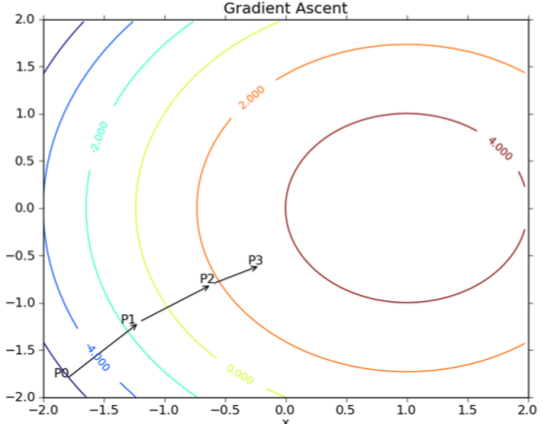
梯度上升算法每次更新之后，都会重新估计移动的方法，即梯度。

Logistic 回归梯度上升优化法

加载数据

1
2
3
4
5
6
7
8
def loadDataSet():
    dataMat = []; labelMat = []
    fr = open('testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat,labelMat
1
2
3
4
5
dataArray, labelMat = loadDataSet()
print("Total: ", len(dataArray))
print("The first sample: ", dataArray[0])
print("The second sample: ", dataArray[1])
print("Label: ", labelMat)
('Total: ', 100)
('The first sample: ', [1.0, -0.017612, 14.053064])
('The second sample: ', [1.0, -1.395634, 4.662541])
('Label: ', [0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0])

数据集梯度上升

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def sigmoid(inX):
    return 1.0/(1+np.exp(-inX))

def gradAscent(dataMatIn, classLabels):
    dataMatrix = np.mat(dataMatIn)             #convert to NumPy matrix
    labelMat = np.mat(classLabels).transpose() #convert to NumPy matrix
    m,n = np.shape(dataMatrix)
    alpha = 0.001
    maxCycles = 500
    weights = np.ones((n,1))
    for k in range(maxCycles):              #heavy on matrix operations
        h = sigmoid(dataMatrix*weights)     #matrix mult
        error = (labelMat - h)              #vector subtraction
        weights = weights + alpha * dataMatrix.transpose()* error #matrix mult
    return weights
1
gradAscent(dataArray, labelMat)
matrix([[ 4.12414349],
        [ 0.48007329],
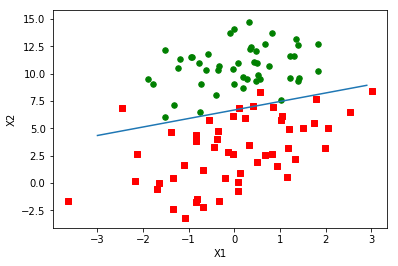
        [-0.6168482 ]])

绘制数据和决策边界

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def plotBestFit(weights):
    import matplotlib.pyplot as plt
    dataMat,labelMat=loadDataSet()
    dataArr = np.array(dataMat)
    n = np.shape(dataArr)[0] 
    xcord1 = []; ycord1 = []
    xcord2 = []; ycord2 = []
    for i in range(n):
        if int(labelMat[i])== 1:
            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
        else:
            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
    ax.scatter(xcord2, ycord2, s=30, c='green')
    x = np.arange(-3.0, 3.0, 0.1)
    y = (-weights[0]-weights[1]*x)/weights[2]
    ax.plot(x, y)
    plt.xlabel('X1'); plt.ylabel('X2');
    plt.show()
1
2
weights = gradAscent(dataArray, labelMat)
plotBestFit(weights.getA())
png

１个epoch的随机梯度上升

梯度上升算法在每次更新系数的时候都需要便利整个数据集，如果数据集的样本比较大，该方法的复杂度和计算代价就很高。有一种改进的方法叫做随机梯度上升方法。该方法的思想是选取一个样本，计算该样本的梯度，更新系数，再选取下一个样本。

1
2
3
4
5
6
7
8
9
def stocGradAscent0(dataMatrix, classLabels):
    m,n = np.shape(dataMatrix)
    alpha = 0.01
    weights = np.ones(n)   #initialize to all ones
    for i in range(m):
        h = sigmoid(sum(dataMatrix[i]*weights))
        error = classLabels[i] - h
        weights = weights + alpha * error * dataMatrix[i]
    return weights
1
2
weights = stocGradAscent0(np.array(dataArray), labelMat)
plotBestFit(weights)
png

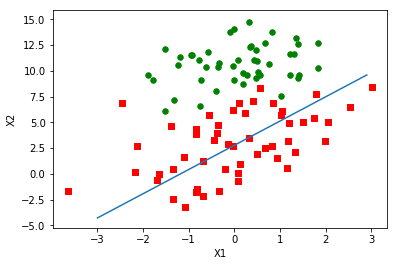
上图之后遍历了一次数据集，这样的模型还处于欠拟合状态。需要多次遍历数据集才能优化好模型，接下来我们会运行200次迭代。

200个epoch的随机梯度上升

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def stocGradAscent0(dataMatrix, classLabels):
    X0, X1, X2 = [], [], []
    m,n = np.shape(dataMatrix)
    alpha = 0.01
    weights = np.ones(n)   #initialize to all ones
    for j in range(200):
        for i in range(m):
            h = sigmoid(sum(dataMatrix[i]*weights))
            error = classLabels[i] - h
            weights = weights + alpha * error * dataMatrix[i]
            X0.append(weights[0])
            X1.append(weights[1])
            X2.append(weights[2])
    return weights, X0, X1, X2
1
2
weights, X0, X1, X2 = stocGradAscent0(np.array(dataArray), labelMat)
plotBestFit(weights)
png

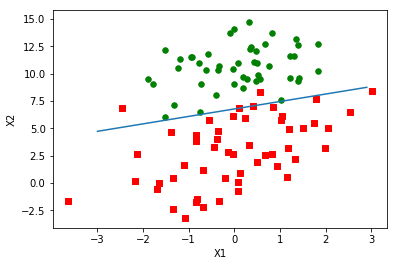
可视化权重(weights)的变化

1
2
3
4
5
fig, ax = plt.subplots(3, 1, figsize=(10, 5))
ax[0].plot(np.arange(len(X0)), np.array(X0))
ax[1].plot(np.arange(len(X1)), np.array(X1))
ax[2].plot(np.arange(len(X2)), np.array(X2))
plt.show()
png

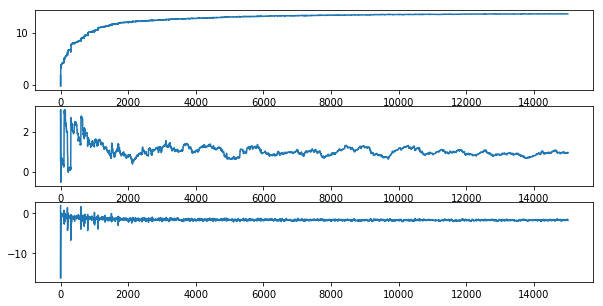
从上图可以看出，算法正在逐渐收敛。由于数据集并不是线性可分的，所以存在一些不能正确分类的样本点，每次更新权重引起了周期的变化。

更新过后的随机梯度上升算法

  1. 学习率alpha会在每次迭代之后调整。
  2. 采用随机选取样本的更新策略，减少周期性的波动。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
    X0, X1, X2 = [], [], []
    m,n = np.shape(dataMatrix)
    weights = np.ones(n)   #initialize to all ones
    for j in range(numIter):
        dataIndex = range(m)
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.0001    #apha decreases with iteration, does not 
            randIndex = int(np.random.uniform(0,len(dataIndex)))#go to 0 because of the constant
            h = sigmoid(sum(dataMatrix[randIndex]*weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            X0.append(weights[0])
            X1.append(weights[1])
            X2.append(weights[2])
            del(dataIndex[randIndex])
    return weights, X0, X1, X2
1
2
weights, X0, X1, X2 = stocGradAscent1(np.array(dataArray), labelMat)
plotBestFit(weights)
png

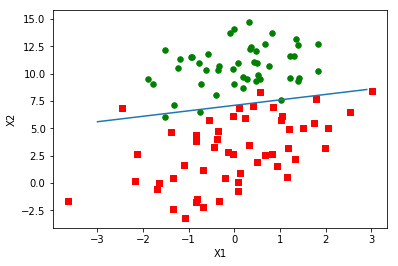
可视化权重(weights)的变化

1
2
3
4
5
fig, ax = plt.subplots(3, 1, figsize=(10, 5))
ax[0].plot(np.arange(len(X0)), np.array(X0))
ax[1].plot(np.arange(len(X1)), np.array(X1))
ax[2].plot(np.arange(len(X2)), np.array(X2))
plt.show()
png

示例：从疝气病症预测病马的死亡率

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def classifyVector(inX, weights):
    prob = sigmoid(sum(inX*weights))
    if prob > 0.5: return 1.0
    else: return 0.0

def colicTest():
    frTrain = open('horseColicTraining.txt', 'r'); frTest = open('horseColicTest.txt', 'r')
    trainingSet = []; trainingLabels = []
    for line in frTrain.readlines():
        currLine = line.strip().split('\t')
        lineArr =[]
        for i in range(21):
            lineArr.append(float(currLine[i]))
        trainingSet.append(lineArr)
        trainingLabels.append(float(currLine[21]))
    trainWeights, X0, X1, X2 = stocGradAscent1(np.array(trainingSet), trainingLabels, 1000)
    errorCount = 0; numTestVec = 0.0
    for line in frTest.readlines():
        numTestVec += 1.0
        currLine = line.strip().split('\t')
        lineArr =[]
        for i in range(21):
            lineArr.append(float(currLine[i]))
        if int(classifyVector(np.array(lineArr), trainWeights))!= int(currLine[21]):
            errorCount += 1
    errorRate = (float(errorCount)/numTestVec)
    print "the error rate of this test is: %f" % errorRate
    return errorRate

def multiTest():
    numTests = 10; errorSum=0.0
    for k in range(numTests):
        errorSum += colicTest()
    print "after %d iterations the average error rate is: %f" % (numTests, errorSum/float(numTests))
1
multiTest()
/home/tianliang/anaconda2/lib/python2.7/site-packages/ipykernel_launcher.py:2: RuntimeWarning: overflow encountered in exp
  


the error rate of this test is: 0.328358
the error rate of this test is: 0.432836
the error rate of this test is: 0.388060
the error rate of this test is: 0.373134
the error rate of this test is: 0.373134
the error rate of this test is: 0.447761
the error rate of this test is: 0.343284
the error rate of this test is: 0.313433
the error rate of this test is: 0.328358
the error rate of this test is: 0.462687
after 10 iterations the average error rate is: 0.379104